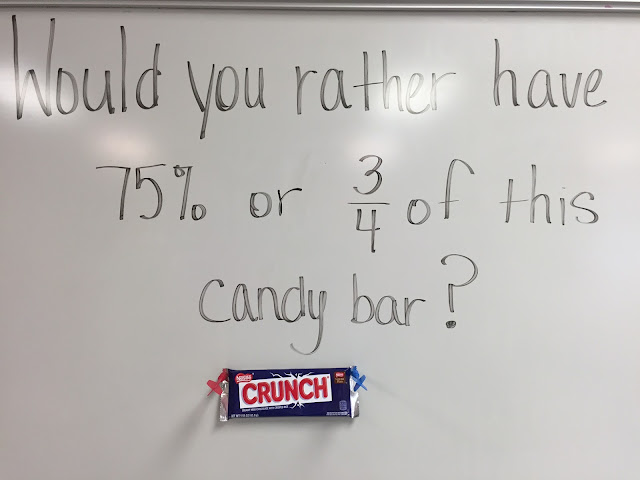Thursday, March 31, 2016
Tuesday, March 29, 2016
FINDING THE AREA OF COMPOSITE FIGURES
Area of a triangle = 1/2 (base x height)
Area of square/rectangle/parallelogram = base x height
Students are going to want to "break up" the figure into triangles and squares/rectangles/parallelograms so they can apply the correct formula.
Remember to number each piece you create and then calculate the areas separately.
All all the areas together to get the total area for the figure.

TANGRAMS, COMPOSITE FIGURES, & AREA OH MY!
Each student was given a set of Tangrams. They were instructed to
- Choose 4 of the pieces and create a figure.
- Trace the figure on page 66 of their math notebook.
- Examine the figure and tell how they could calculate the area of their shape. (Most students were very perplexed. However after some discussion they began to realize they had the proper tools necessary to actually do this.)
- Trace each individual shape within their figure. (At this point most students began to realize they could find the area of each piece and then total up the area)
- Number each piece in the figure.
I then gave the students the base and height measurements for each shape.
- small triangle - b=3cm h=2cm
- medium triangle - b=5cm h=4cm
- large triangle - b=8cm h=8cm
- parallelogram - b=3cm h=2cm
- square - b=3 h=3
Students were then asked to calculate the area of each piece they used in their figure. Next they added up the total area of all pieces to get the area of their composite figure. Below is an example from a student math notebook.
In conclusion students learned they are able to "Break up" the figure to make squares and triangles. These are the only 2 formulas they are using currently to find the area.
Monday, March 28, 2016
3/28 PRACTICE & HOMEWORK
BONUS - TYPE OF TRIANGLE
Triangles have a First, Middle, and Last Name
Their First name is based on their sides
Their Middle name is based on their angles
Their Last name is Triangle (LOL)
Side Names:
Equilateral - all sides have equal length
Scalene - all sides have different lengths
Isosceles - 2 sides have equal lengths
Angle Names:
Right - one angle is 90 degrees (right angle)
Acute - all angles are less than 90 degrees
Obtuse - one angle is greater than 90 degrees
Thursday, March 24, 2016
Monday, March 21, 2016
STUDY GUIDE ANSWERS
1.) 3/4
3.) 3/50
5.) .20 20%
7.) .625 62.5%
11.) .006 3/500
12.) .228 57/250
16.
a. 3:4
b. 4:3
c. 1:1
d. 3:10
e. Many possible answers: 4:3 16:12 24:18
17.) 6 shirts at $17.99
18.) 1:3
19.) 40 girls
20.) 45 km
22.) 4 miles per hour
23.) 19 cars per day
25.)8
34.) 54
35.) 130
38.) 20
39.) 25
42.) 70
43.) 200
56.) 300 feet
57.) 68000 pounds
58.) .127 m
59.) 6,000,000 L
60.) 14.2 kg
3.) 3/50
5.) .20 20%
7.) .625 62.5%
11.) .006 3/500
12.) .228 57/250
16.
a. 3:4
b. 4:3
c. 1:1
d. 3:10
e. Many possible answers: 4:3 16:12 24:18
17.) 6 shirts at $17.99
18.) 1:3
19.) 40 girls
20.) 45 km
22.) 4 miles per hour
23.) 19 cars per day
25.)8
34.) 54
35.) 130
38.) 20
39.) 25
42.) 70
43.) 200
56.) 300 feet
57.) 68000 pounds
58.) .127 m
59.) 6,000,000 L
60.) 14.2 kg
Friday, March 18, 2016
Thursday, March 17, 2016
3/17/2016 HOMEWORK
Very thankful to have great resources available on the internet. I really like the worksheets from this site: homeschoolMath.net/worksheets
Tuesday, March 15, 2016
Friday, March 11, 2016
PERCENT VIDEO (THINKING ENCOURAGED)
*There is a mistake in the first question! It should read "What is 20% of 80?"
Thursday, March 10, 2016
PERCENTS
 |
| Add caption |
 |
| 85/100 |
 |
| "I must write the number over 100" |
 |
| 27% |
 |
| "I must read the decimal in word form to help me write it as a fraction over 100. Then I will have the percent, because all percents are a number over 100. |
 |
| The decimal point is being moved 2 places to the right every time. |
 |
| 4/5 as a percent is 80%. I changed 4/5 to 80/100 by multiplying the numerator and denominator by 20. Then I got 80% because 80 over 100 is 80%. |
 |
| #1 - 46% = 46/100 = 23/50 #2 - 128% = 128/100 = 32/25 = 1 7/25 |
 |
| #1 - .01 x 78 = .78 or 1/100 x 78/1 = 39/50 = .78 #2 - .25 x 40 = 10 or 25/100 x 40/1 = 10 #3 - 1 x 78 = 78 or 100/100 x 78/1 = 78 #4 - .50 x 62 = 31 or 50/100 x 62/1 = 31 |
Friday, March 4, 2016
USING TABLES & PROPORTIONS TO SOLVE PROBLEMS
The following picture is of the class assignment. #1 and #4 have been done for the class to help them figure the remainder of the paper out.
Tuesday, March 1, 2016
RATES
Click the link to watch a short video descirbing Rates
LearnZillion
After the video everyone shared the notes they had taken. Below is the list I compiled.
In class we practiced determining if a ratio was a rate or a unit rate using right arm/left arm to share our answers. The following questions were used for practice.
LearnZillion
After the video everyone shared the notes they had taken. Below is the list I compiled.
In class we practiced determining if a ratio was a rate or a unit rate using right arm/left arm to share our answers. The following questions were used for practice.
Subscribe to:
Posts (Atom)